ESTADÍSTICA
RECUENTO DE DATOS
FRECUENCIAS
Para manejar los resultados de una encuesta, de una votación o de cualquier estudio estadístico, lo primero que hemos de hacer es organizar los resultados obtenidos, ordenándolos y clasificándolos, es decir, haciendo lo que se llama un recuento de los datos.
FRECUENCIA ABSOLUTA
Se llama frecuencia absoluta de un dato al número de veces que ha salido ese dato o resultado.
La suma de las frecuencias absolutas de todos los datos que se han obtenido en la encuesta o estudio, ha de ser igual al número total de datos.
Vamos a hacer un recuento de datos y a ver su frecuencia relativa en el ejemplo siguiente: Hemos preguntado a los 22 alumnos y alumnas de clase sobre cuál será el resultado del próximo derby entre dos clubes de fútbol rivales, obteniendo estos resultados:
1 - 2 - X - X - 1 - 1 - 2 - X - 1 - 1 - X - 2 - 1 - 1 - 1 - X - X - 2 - 1 - 2 - 2 – X
donde el 1 significa que gana el equipo de casa, la X que empatan y el 2 que gana el equipo visitante.
Efectuamos el recuento de los datos, anotando el número de veces que ha aparecido cada uno de los resultados.
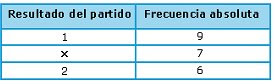
Ahora construiríamos una tabla, llamada tabla de frecuencias, en la que pondríamos en la segunda columna las frecuencias absolutas:
La suma de las frecuencias absolutas es: 9 + 7 + 6 = 22
Lo primero que hemos de hacer es comprobar que no nos hemos dejado ningún resultado sin contar: en este caso hemos preguntado a 22 alumnos de clase, que coincide con el resultado de la suma anterior.
Estas tablas son una forma sencilla de presentar los datos y hacen más fácil interpretar los resultados.
FRECUENCIA RELATIVA
Se llama frecuencia relativa de un dato al cociente entre su frecuencia absoluta y el número total de datos.
La suma de todas las frecuencias relativas de los datos de un estudio tiene que ser igual a 1.
Para los resultados de la encuesta anterior, escribimos una nueva columna a la derecha de la tabla de frecuencias en la que vamos calculando cada una de las frecuencias relativas:
La suma de las frecuencias absolutas es: 9 + 7 + 6 = 22
La suma de las frecuencias relativas es:
Hay una mayoría que piensan que ganará el equipo de casa, el resultado 1.
Veamos ahora otro ejemplo: Hemos hecho una votación entre los 22 alumnos y alumnas para elegir de entre cuatro candidatos al delegado de nuestra clase, obteniéndose los siguientes resultados:
Carlos - Paula – Carmen – Ana – Carmen – Paula – Paula – Carlos – Ana – Paula – Carlos – Paula – Ana – Carmen - Paula – Carmen – Carlos – Carlos – Paula – Carlos - Paula – Carmen
Hacemos, en primer lugar, el recuento de los datos:
Una vez efectuado el recuento, construimos la tabla de frecuencias:
La suma de las frecuencias absolutas es: 6 + 8 + 5 + 3 = 22
La suma de las frecuencias relativas es:
La más votada ha sido Paula, que será la delegada de clase.








No hay comentarios:
Publicar un comentario